Zadani su vrhovi trokuta, pronađite visinu. Zadane su koordinate vrhova trokuta ABC

Primjer rješavanja nekih zadataka iz standardnog rada “Analitička geometrija u ravnini”

Zadani su vrhovi,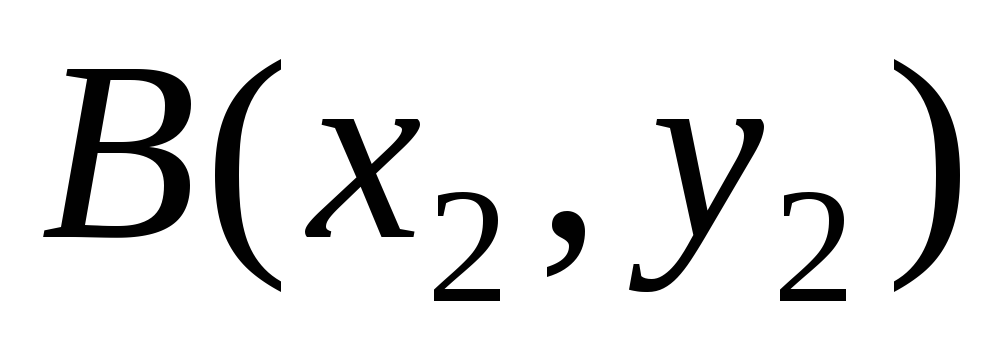

,

trokut ABC. Pronaći:

Jednadžbe svih stranica trokuta;

Sustav linearnih nejednadžbi koje definiraju trokut ABC;

Jednadžbe visine, medijane i simetrale trokuta povučene iz vrha A;

Sjecište visina trokuta;

Sjecište središnjica trokuta;

Duljina visine spuštena u stranu AB;

Kutak A;

Napravite crtež.

Neka vrhovi trokuta imaju koordinate: A (1; 4), U (5; 3), S(3; 6). Odmah nacrtajmo crtež:

1. Za zapis jednadžbi svih stranica trokuta koristimo jednadžbu pravca koji prolazi kroz dvije zadane točke s koordinatama ( x 0 , g 0 ) i ( x 1 , g 1 ):

=

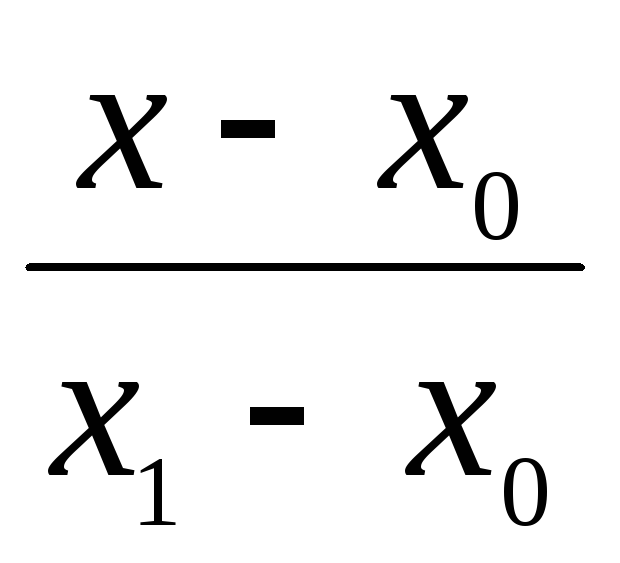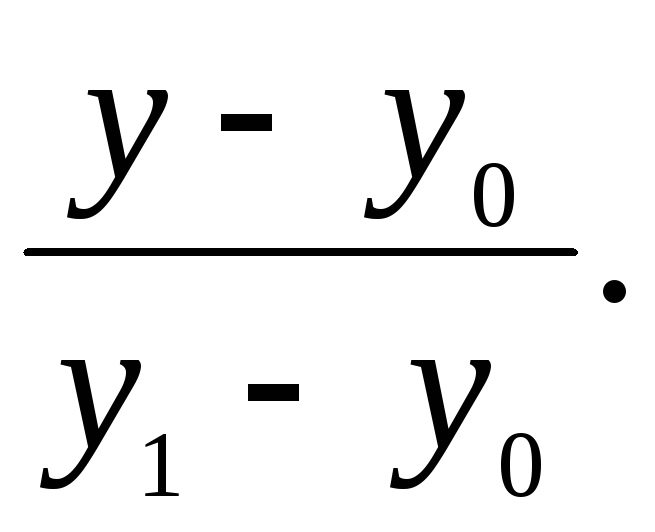
Dakle, zamjenom umjesto ( x 0 , g 0 ) koordinate točke A, a umjesto ( x 1 , g 1 ) koordinate točke U, dobivamo jednadžbu pravca AB:

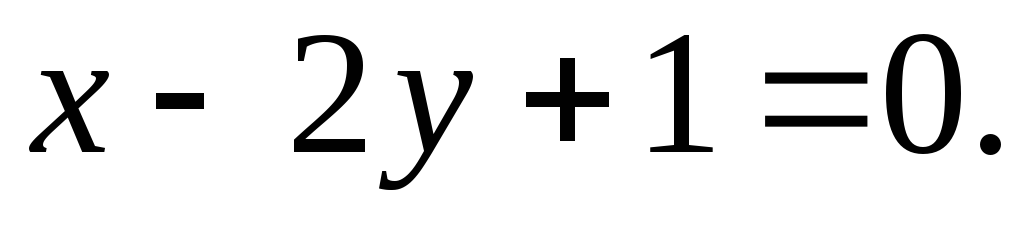
Rezultirajuća jednadžba će biti jednadžba pravca AB, napisano u opći oblik. Slično, nalazimo jednadžbu ravne linije AC:

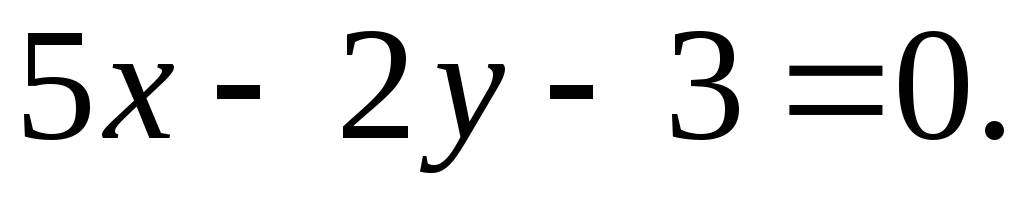
I također jednadžba ravne linije Sunce:

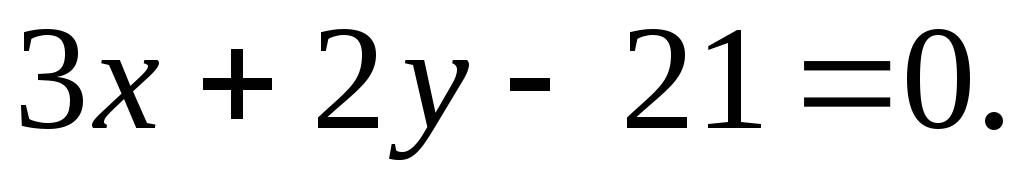
2. Uočimo da skup točaka trokuta ABC predstavlja presjek triju poluravnina, a svaka se poluravnina može definirati pomoću linearne nejednadžbe. Ako uzmemo jednadžbu bilo koje strane ∆ ABC, Na primjer AB, zatim nejednakosti

I

definirati točke koje leže na suprotnim stranama pravca AB. Trebamo odabrati poluravninu u kojoj leži točka C. Zamijenimo njene koordinate u obje nejednadžbe:

Druga nejednadžba će biti točna, što znači da su tražene točke određene nejednadžbom

.

Isto radimo s ravnom linijom BC, njezinom jednadžbom

. Koristimo točku A (1, 1) kao ispitnu točku:

To znači da tražena nejednakost ima oblik:

.

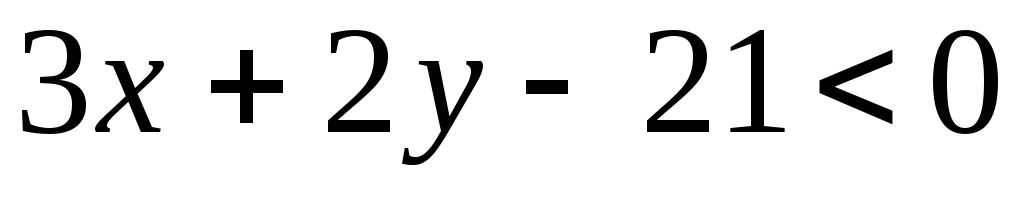Ako provjerimo ravnu liniju AC (ispitna točka B), dobivamo:

To znači da će tražena nejednakost imati oblik

Konačno dobivamo sustav nejednakosti:

Znakovi “≤”, “≥” znače da su točke koje leže na stranicama trokuta također uključene u skup točaka koje čine trokut ABC.

3. a) Da bismo pronašli jednadžbu za visinu ispuštenu s vrha A na stranu Sunce, razmotrite jednadžbu stranice Sunce:

.

Vektor s koordinatama Sunce okomito na stranu A pa prema tome paralelno s visinom. Zapišimo jednadžbu pravca koji prolazi točkom

:

paralelno s vektorom A Ovo je jednadžba za visinu izostavljena iz t. Sunce.

na stranu Sunce b) Odredi koordinate sredine stranice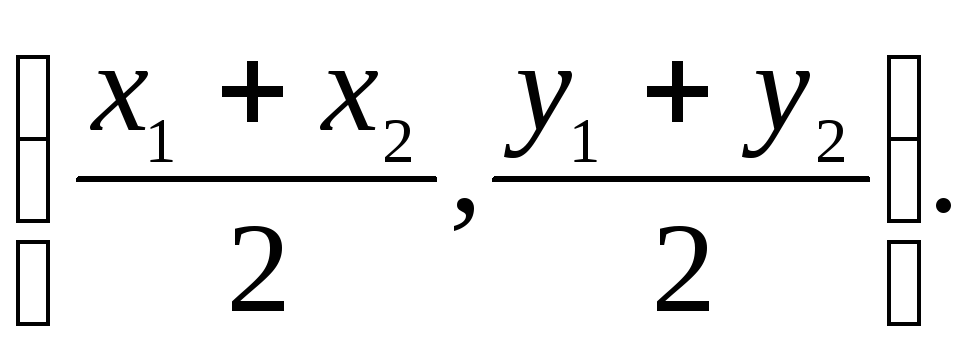

prema formulama: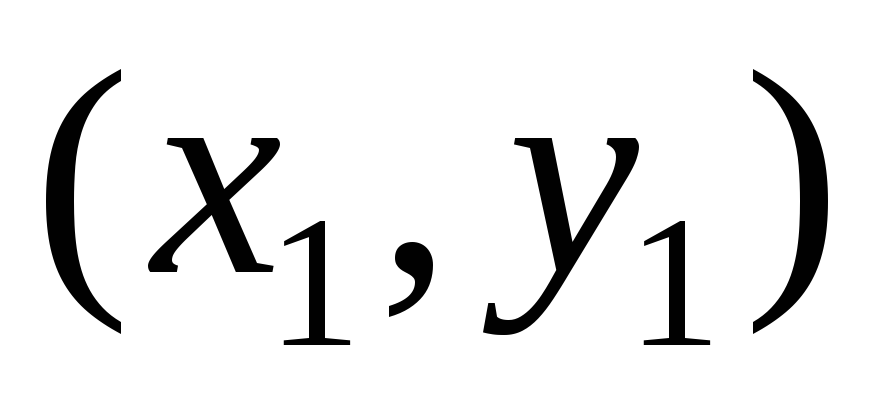

Ovdje U- to su koordinate t.

, A S. Zamijenimo i dobijemo:

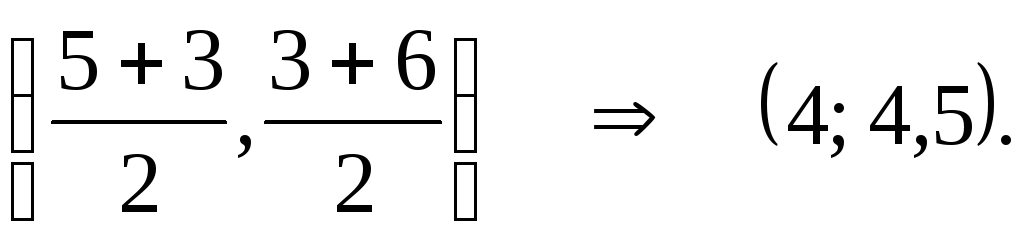
Pravac koji prolazi ovom točkom i točkom A je traženi medijan:

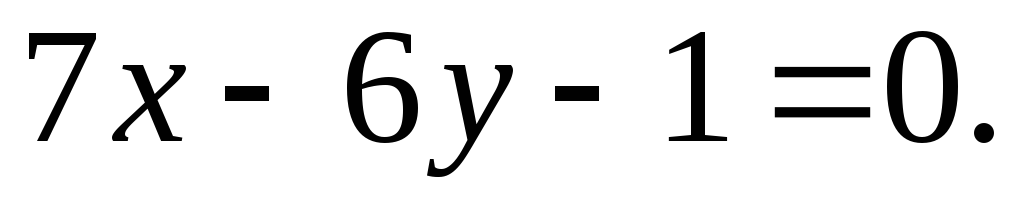
c) Jednadžbu simetrale tražit ćemo na temelju činjenice da su u jednakokračnom trokutu visina, središnja i simetrala spuštene iz jednog vrha na osnovicu trokuta jednake. Nađimo dva vektora

I

i njihove duljine:

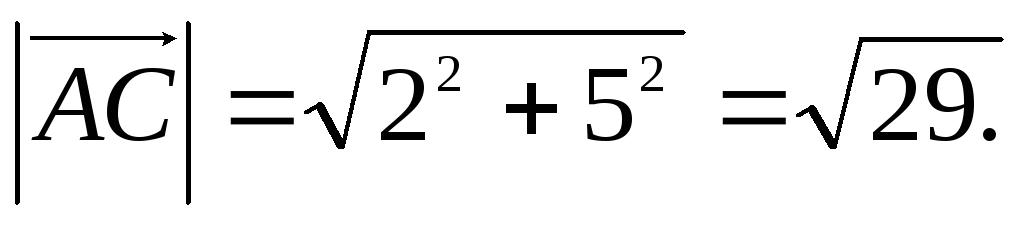
Zatim vektor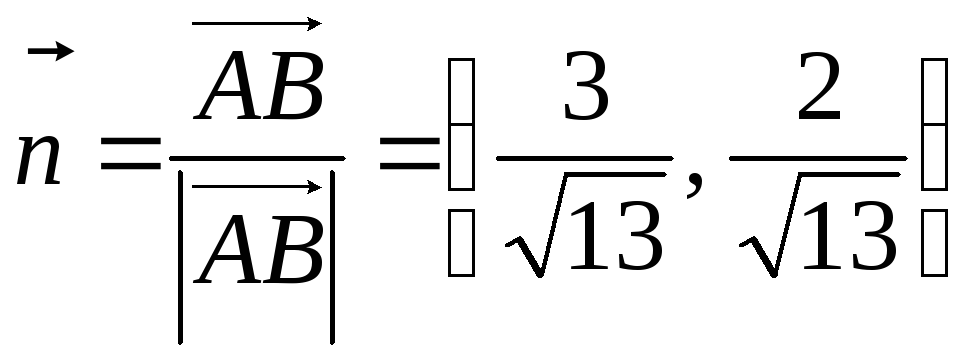

ima isti smjer kao vektor

, i njegovu duljinu

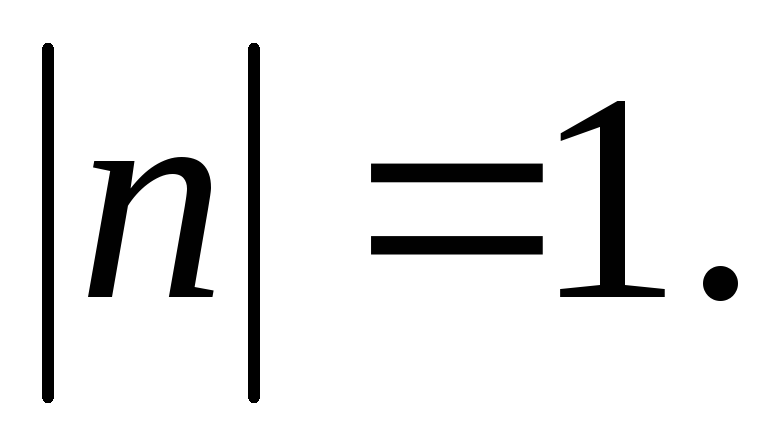Isto tako, jedinični vektor

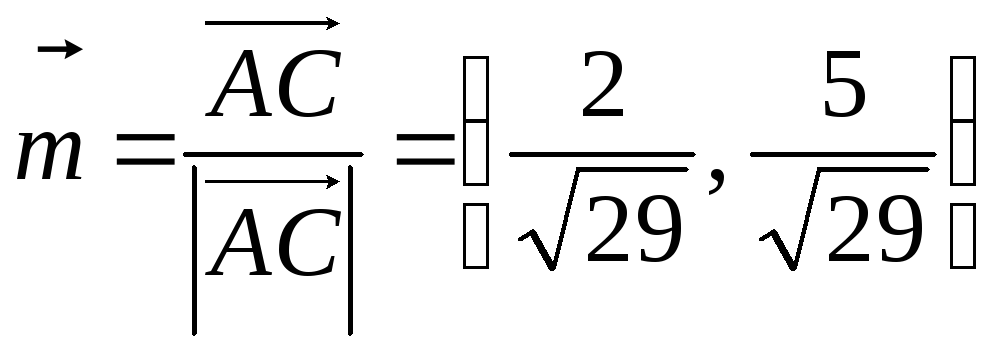poklapa se po smjeru s vektorom

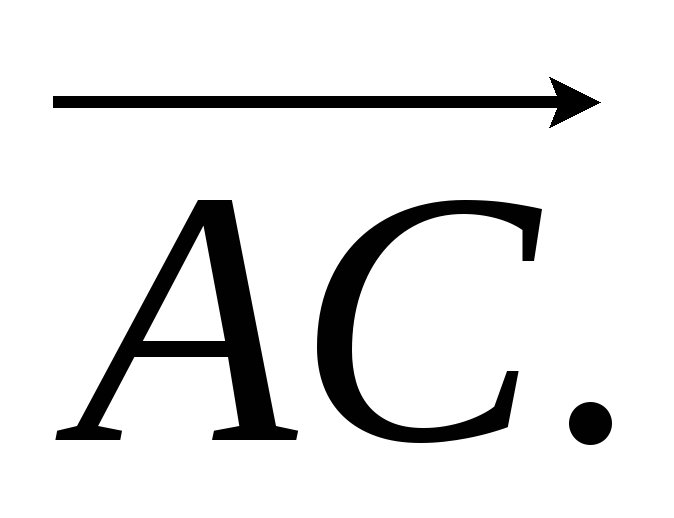Vektorski zbroj

postoji vektor koji se po smjeru podudara sa simetralom kuta A. Dakle, jednadžba željene simetrale može se napisati kao:

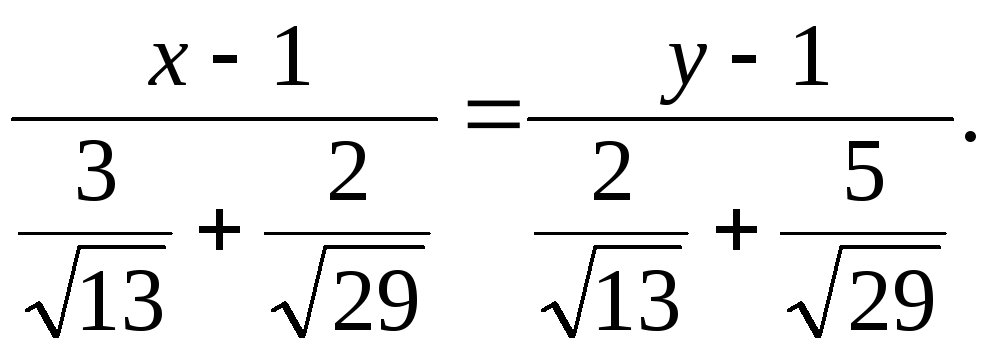
4) Već smo konstruirali jednadžbu za jednu od visina. Konstruirajmo jednadžbu za drugu visinu, na primjer, iz vrha U. Strana AC zadan jednadžbom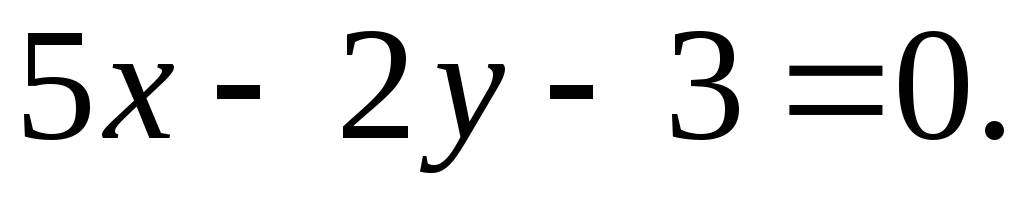

Dakle, vektor

okomito AC, a time i paralelno sa željenom visinom. Zatim jednadžba pravca koji prolazi kroz vrh U u smjeru vektora

(tj. okomito AC), ima oblik:

Poznato je da se visine trokuta sijeku u jednoj točki. Konkretno, ova točka je sjecište pronađenih visina, t.j. rješavanje sustava jednadžbi:

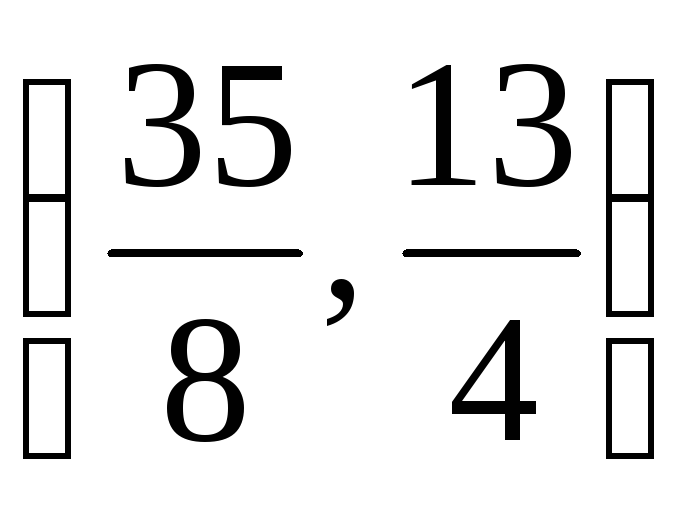- koordinate ove točke.

5. Sredina AB ima koordinate

. Napišimo jednadžbu medijana na strani AB. Ovaj pravac prolazi kroz točke s koordinatama (3, 2) i (3, 6), što znači da njegova jednadžba ima oblik:

Imajte na umu da nula u nazivniku razlomka u jednadžbi pravca znači da je taj pravac paralelan s ordinatnom osi.

Da bismo pronašli sjecište medijana, dovoljno je riješiti sustav jednadžbi:

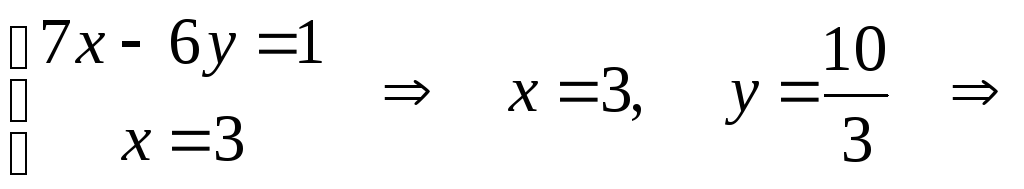
Sjecište središnjica trokuta ima koordinate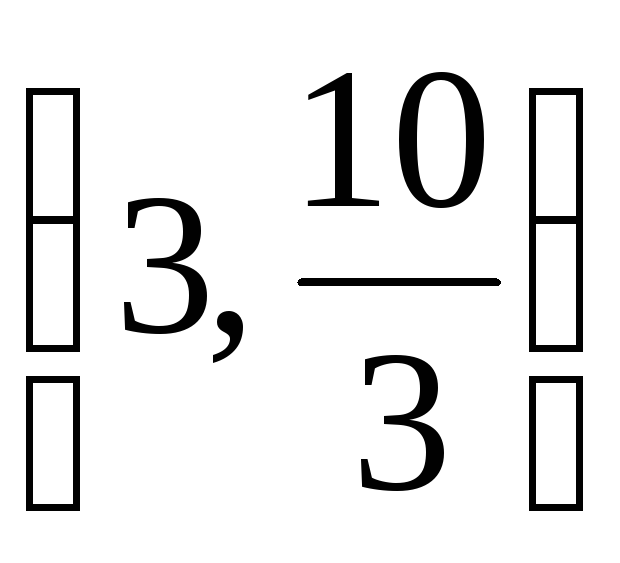

.

6. Duljina visine spuštena u stranu AB, jednaka udaljenosti od točke S na ravnu liniju AB s jednadžbom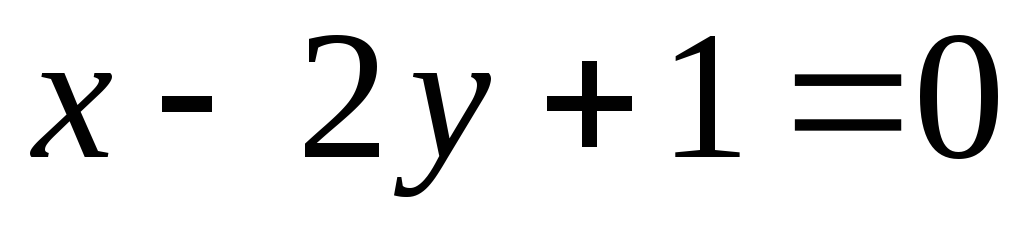

a nalazi se po formuli:

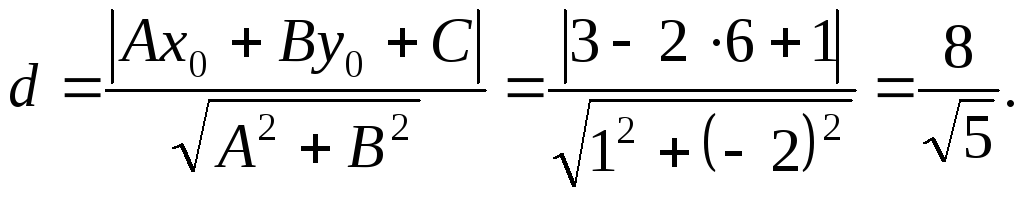
7. Kosinus kuta A može se pronaći pomoću formule za kosinus kuta između vektora I 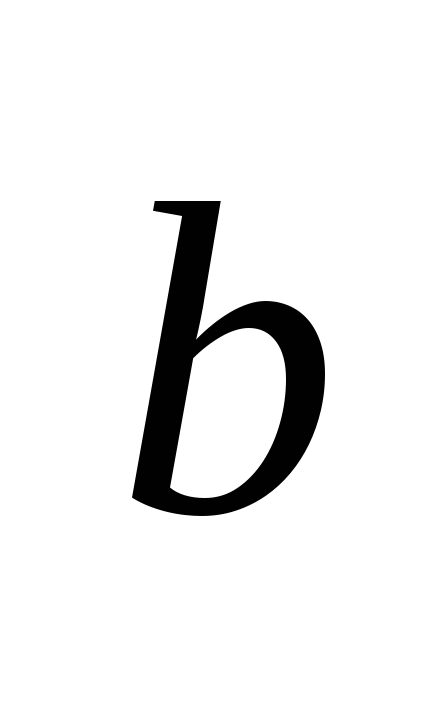, koji je jednak omjeru skalarnog umnoška ovih vektora i umnoška njihovih duljina:

.

sažetak ostalih prezentacija

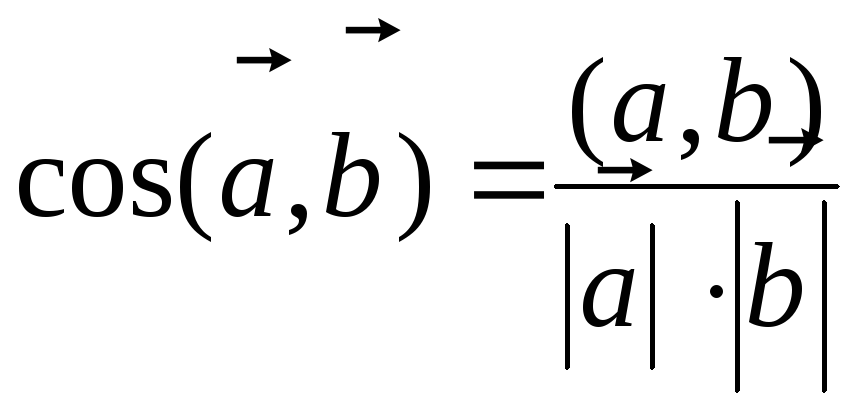“Algoritamske konstrukcije” - Složeni algoritam. Algoritam za rješavanje problema. Grafički način prikazivanja algoritama. Lijepljenje tapeta. Algoritamski dizajni. Blok dijagram. Algoritam. Metode prezentiranja algoritama. Ciklus. Predstavljanje algoritama u obliku opisa slijeda radnji. Dijagram toka algoritma "Pozadinske slike". Skup tipičnih struktura. Blok dijagrami osnovnih struktura. Oblici prikaza algoritama. Način predstavljanja algoritama u obliku grafikona.

“Glavne vrste algoritamskih struktura” - grananje. Pravopis prefiksa. Glavni tipovi agroritmičkih struktura. Algoritam. Postavljanje početnih parametara. Recept za pripremu čaja. Struktura. Blok znakova. Napiši algoritme u verbalnom obliku. Ciklus. Ciklusi. Zadaci za učvršćivanje znanja. Algoritam grananja. Osnovna struktura. Kraj algoritma. Petlja s postuvjetom. Osnovni tipovi algoritamskih struktura. Rad u grupama. Uvjetna petlja.

"Osnovne algoritamske strukture" - razumljivost i izvedivost. Primjeri algoritama koje poznajete. Algoritam se može prikazati na različite načine. Kako se izvršavaju naredbe u linearnom algoritmu. Grananje. Učinkovitost i diskrecija. Svojstva algoritma. Produktivnost. Stanje. Determinizam. Osnovni elementi blok dijagrama. Pojam informacije. Dijeljenje algoritma u niz koraka. Linearni algoritam. Cikličke algoritamske konstrukcije.

“Vrste algoritama” - Algoritmi za snimanje. Uđi u vrt. Uvod u algoritam. Otvori torbu. Hanojski tornjevi. Pogledajte crtić. Moto lekcije. Približite se prijelazu. Žetva žetve. Ciklički algoritmi. Dlanovi. Algoritam ljudskih postupaka. Algoritam. Čišćenje stana. Grafički diktat. Naziv figure.

Kuća je spremna. Što je algoritam? Primarne boje. Momčad. Snimanje ciklusa u postupku. Znanje. Crtanje krova. Promjena boje olovke. Nacrtajmo zid. Idemo crtati. Ciklus. Crtamo prozore. Nacrtajmo kuću. Interaktivni tutorial. Korekcija zahvata.

“Načini pisanja algoritama” - Primjer algoritma. Verbalni način pisanja algoritama. Često korišteni simboli i njihova namjena. Što je algoritam? Preporučljivo je algoritme prikazati u tabelarnom obliku. Oblici prikaza algoritama. Pseudokod. Softverska metoda za pisanje algoritama. Primjer algoritma u SHAYA. Primjer blok dijagrama. Algoritmi su prikazani u grafičkom obliku. Metode pisanja algoritama.

Problem 1. Zadane su koordinate vrhova trokuta ABC: A(4; 3), B(16;-6), C(20; 16). Odredi: 1) duljinu stranice AB; 2) jednadžbe stranica AB i BC i njihovih kutnih koeficijenata; 3) kut B u radijanima s točnošću od dvije znamenke; 4) jednadžba visine CD i njezine duljine; 5) jednadžbu središnje AE i koordinate točke K sjecišta ove središnje s visinom CD; 6) jednadžba pravca koji prolazi točkom K paralelno sa stranicom AB; 7) koordinate točke M, smještene simetrično na točku A u odnosu na ravnu liniju CD.

Otopina:

1. Udaljenost d između točaka A(x 1 ,y 1) i B(x 2 ,y 2) određena je formulom

Primjenom (1) nalazimo duljinu stranice AB:

2. Jednadžba pravca koji prolazi kroz točke A(x 1 ,y 1) i B(x 2 ,y 2) ima oblik

(2)

Zamjenom koordinata točaka A i B u (2) dobivamo jednadžbu stranice AB:

Nakon što smo riješili posljednju jednadžbu za y, nalazimo jednadžbu stranice AB u obliku jednadžbe ravne linije s kutnim koeficijentom:

Zamjenom koordinata točaka B i C u (2) dobivamo jednadžbu pravca BC:

3. Poznato je da se tangens kuta između dviju ravnih linija, čiji su kutni koeficijenti jednaki, izračunava po formuli

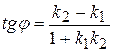(3)

Traženi kut B tvore prave linije AB i BC, čiji kutni koeficijenti se nalaze: Primjenom (3) dobivamo

Ili drago.

4. Jednadžba pravca koji prolazi zadanom točkom u zadanom smjeru ima oblik

(4)

Visina CD okomita je na stranicu AB. Da bismo pronašli nagib visine CD, koristimo uvjet okomitosti pravaca. Od tada Zamjenjujući u (4) koordinate točke C i pronađeni kutni koeficijent visine, dobivamo

Da bismo pronašli duljinu visine CD, najprije odredimo koordinate točke D - sjecišta pravaca AB i CD. Zajedničko rješavanje sustava:

nalazimo tj. D(8;0).

Pomoću formule (1) nalazimo duljinu visine CD:

5. Da bismo pronašli jednadžbu medijane AE, najprije odredimo koordinate točke E, koja je sredina stranice BC, koristeći formule za dijeljenje segmenta na dva jednaka dijela:

(5)

Stoga,

Zamjenom koordinata točaka A i E u (2) nalazimo jednadžbu za medijan:

Da bismo pronašli koordinate sjecišta visine CD i medijane AE, zajedno rješavamo sustav jednadžbi

Nalazimo.

6. Budući da je tražena pravac paralelna sa stranicom AB, njezin će kutni koeficijent biti jednak kutnom koeficijentu pravca AB. Zamjenom u (4) koordinate nađene točke K i kutni koeficijent dobivamo

3x + 4y – 49 = 0 (KF)

7. Kako je pravac AB okomit na pravac CD, tražena točka M, koja se nalazi simetrično točki A u odnosu na pravac CD, leži na pravcu AB. Osim toga, točka D je središte segmenta AM. Koristeći formule (5), nalazimo koordinate željene točke M:

Trokut ABC, visina CD, središnja AE, pravac KF i točka M konstruirani su u xOy koordinatnom sustavu na sl. 1.

Zadatak 2. Napravite jednadžbu za geometrijsko mjesto točaka čije su udaljenosti do zadane točke A(4; 0) i zadanog pravca x=1 jednake 2.

Otopina:

U koordinatnom sustavu xOy konstruiramo točku A(4;0) i pravac x = 1. Neka je M(x;y) proizvoljna točka željenog geometrijskog mjesta točaka. Spustimo okomicu MB na zadani pravac x = 1 i odredimo koordinate točke B. Kako točka B leži na zadanom pravcu, njena apscisa je jednaka 1. Ordinata točke B jednaka je ordinati točke M. Prema tome, B(1;y) (slika 2).

Prema uvjetima zadatka |MA|: |MV| = 2. Udaljenosti |MA| i |MB| nalazimo iz formule (1) problema 1:

Kvadrirajući lijevu i desnu stranu, dobivamo

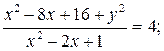
Rezultirajuća jednadžba je hiperbola u kojoj je realna poluos a = 2, a imaginarna poluos

Definirajmo žarišta hiperbole. Za hiperbolu, jednakost je zadovoljena, i – trikovi hiperbola. Kao što vidite, dana točka A(4;0) je desni fokus hiperbole.

Odredimo ekscentricitet rezultirajuće hiperbole:

Jednadžbe asimptota hiperbole imaju oblik i . Prema tome, ili i su asimptote hiperbole. Prije konstruiranja hiperbole konstruiramo njezine asimptote.

Problem 3. Napravite jednadžbu za geometrijsko mjesto točaka jednako udaljenih od točke A(4; 3) i pravca y = 1. Svedite dobivenu jednadžbu na njen najjednostavniji oblik.

Otopina: Neka je M(x; y) jedna od točaka željenog geometrijskog mjesta točaka. Spustimo okomicu MB iz točke M na ovu ravnicu y = 1 (slika 3). Odredimo koordinate točke B. Očito je da je apscisa točke B jednaka apscisi točke M, a ordinata točke B jednaka je 1, tj. B(x; 1). Prema uvjetima zadatka |MA|=|MV|. Prema tome, za bilo koju točku M(x;y) koja pripada željenom geometrijskom mjestu točaka vrijedi sljedeća jednakost:

Rezultirajuća jednadžba definira parabolu s vrhom u točki. Da bismo jednadžbu parabole doveli do njezinog najjednostavnijeg oblika, postavimo i y + 2 = Y, tada jednadžba parabole ima oblik:

Da bismo konstruirali pronađenu krivulju, pomaknemo ishodište koordinata u točku O"(4;2), konstruiramo novi koordinatni sustav čije su osi redom paralelne s osi Ox i Oy, a zatim u tom novom sustavu konstruiramo parabolu ( *) (slika 3).

Problem 4. Sastavite kanoničku jednadžbu hiperbole čiji se fokusi nalaze na x-osi ako ona prolazi točkama A(-8;12) i B(12;8). Pronađite sve točke presjeka ove hiperbole s kružnicom sa središtem u ishodištu, ako ta kružnica prolazi kroz žarišta hiperbole.

Otopina: Kanonska jednadžba hiperbole ima oblik

Prema stanju točke A I U ležati na hiperboli. Prema tome, koordinate tih točaka zadovoljavaju jednadžbu (1). Zamjena u jednadžbu (1) umjesto trenutnih koordinata X (slika 4).